subzcuber's notes

Priority Queues and Heaps

2 min read

Algorithms #heaps queues

  • Array representation
  • Operations
    • Heapify
    • Making a Heap
    • Insertion
    • Deletion
    • ExtractMax/ExtractMin
    • Heapsort
  • Common Problem Patterns
    • Top K elements
    • Merge K sorted arrays
    • Two Heaps
    • Minimum Number

A heap is a complete binary tree, with each child being either greater (minHeap) or less than (maxHeap) than its parent

Array Representation

Since it a complete binary tree, it can be stored in an array instead of a tree structure

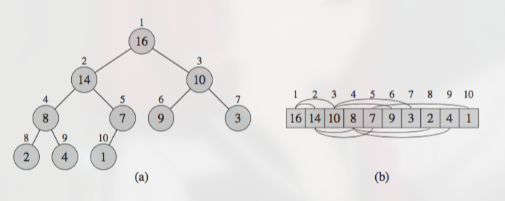
  • root is at heap[0]
  • left subtree of node i is at heap[2i + 1]
  • right subtree of node i is at heap[2i + 2]
  • parent of node i is at heap[(i-1)/2]

Number of Leaves: There are leaves

Operations

Heapify

void heapify(int* heap, int n, int i) {
	if (n <= 1)
		return;
	int largest = i;
	int l = 2*i + 1;
	int r = 2*i + 2;
	if (l < n && heap[l] > heap[largest]) // MaxHeap
		largest = l;
	if(r < n && heap[r] > heap[largest]) // MaxHeap
		largest = r;
	if (i != largest) {
		swap(A[i], A[largest]);
		heapify(heap, n, largest);
	}
}

Making a Heap

for (int i = (n-1)/2; i>=0; i--)
	heapify(heap, n, i);

Insertion

void insert (int* heap, int key) {
	if (A.size == 0) {
		A.append(key);
		return;
	} else {
		A.append(key);
		int i = A.size - 1; // index of newly appended key
		while (i!=0 && heap[(i-1)/2] < heap[i]) {
			swap(heap[i], heap[(i-1)/2]);
			i = (i-1)/2;
		}
	}
}

LEETCODE

506. Relative Ranks

  • store score and index in a heap, sort the heap, return your answers

703. Kth Largest Element in a Stream

Backlinks