Hash Functions and MACs

• properties of hash functions
  • Random Oracle Model
• security requirements
  • preimage resistance (one way)
  • second preimage resistance (weak collision resistance)
  • collision resistance (strong collision resistancce)
• Merkle-Damgard Construction
  • Reductions
  • Iterated Hashes
  • Proof
• MAC
  • Length Extension attack
  • HMAC
  • Encrypted Authentication

Properties

A hash family is a four-tuple $(X,Y,K,H)$ where

• $X$ is a set of possible messages (may be infinite)
• $Y$ is the finite set of possible hashes/digests/tags
• $K$ is the keyspace
• $H$ for each $k\in K$ there is a hash function $h_k\in H$

NOTE

unkeyed hash ⇒ $|K|=1$

The perfect hash function is a random oracle which is impossible to achieve

properties

• arbitrary input size
• fixed output size
• efficiency
• pseudorandomness, i.e. should nto be possible to derive a relation between $h(x)$ and $h(f(x))$
• one way
• computationally impossible to find collision

Security Requirements

Preimage Resistance (One-wayness)

OW

Infeasible to find $x$ such that $h(x)=y$ for a given $y\in \{0,1{\}}^d$ $x$ is the preimage of $y$

Second Preimage Resistance

TCR

given $x_1$ and $h(x_1)$ it should be infeasible to find $x_2$ such that $h(x_2)=h(x_1)$

this is just weak collision resistance

Collision Resistance

CR

infeasible to find a pair $(x,x^{\prime })$ such that $x\ne x;$ and $h(x)=h(x^{\prime })$

Birthday Paradox

just need 23 people for a 50% chance of same birthday $\mathrm{Pr}(\text{no collision in 2 people})=(365-\frac{1}{365})$ $\mathrm{Pr}(\text{no collision in 3 people})=(365-\frac{1}{365})\cdot (365-\frac{2}{365})$ and so on

Number of messages required to find a collision with decent probability

$\mathrm{Pr}(\text{no collision})={\prod }_{i=1}^{t-1}(1-\frac{i}{2^n})$ and $e^{-x}\approx (1-x)$ $\mathrm{Pr}(\text{no collision})={\prod }_{i=1}^{t-1}{e}^{\frac{i}{2^n}}$ $\mathrm{Pr}(\text{no collision})=e^{\frac{-(t-1)t}{2^{(}n+1)}}$ let $\lambda$ = $\mathrm{Pr}(collision)$ $\lambda =1-e^{\frac{-(t-1)t}{2^{(}n+1)}}$ $t(t-1)=2^{n+1}\ln (\frac{1}{1-\lambda })$ and $t(t-1)\approx t^2$ $t\approx \sqrt{2^{n+1}\ln (\frac{1}{1-\lambda })}$

collision finding

$t\approx 2^{\frac{n}{2}}$ hashes needed to find a collision with decent probability

Relation of These Properties

flowchart LR
	A[CR]
	B[SPI]
	C[PI]
	
A --> B 
A --> C

• finding collisions is easier than finding TCR or PI
• $\therefore$ collision resistance ⇒ second preimage resistance and preimage resistance

Reading Further

Discussion of these attacks in terms of graphs, where # of edges is the “number of chances” to get a collision. Collision-resistance brute force is a complete graph (need √N vertices to have N edges / chances for a collision) . Second-preimage brute force is a star graph (need N vertices to N edges). Can generalize to consider complete bipartite graph between √N + √N vertices.

Merkle-Damgard Paradigm

if you have collision resistance function $h(x)$ that compresses from $m+t\to m$ you can expand this to create collision resistant function $H(x)$ that compresses from $\infty \to m$

Iterated Hashes

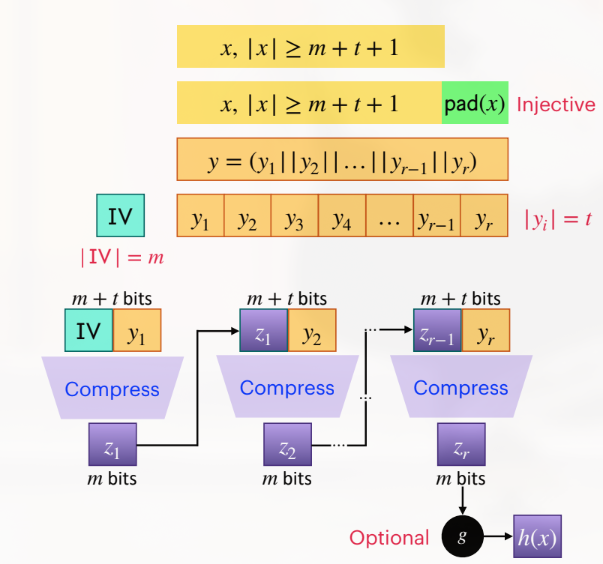
Merkle and Damgard independently proved that if $h(x)$ is collision resistant then $H(x)$ is too. I am NOT proving ts

Message Authentication Codes

keyed cryptographic hash. So you want to hash your key together with your message.

1. IV = key
   • can’t make hash function public or something i think
2. $h(K||x)$ → secret prefix
   • can just append extra blocks with no issue
3. $h(x||K)$ → secret suffix
   • weak to collisions

These are vulnerable to length extension attacks

HMAC is the standard

${\text{HMAC}}_K(x)=\text{SHA-1}((K\oplus opad)||\text{SHA-1}((K\oplus ipad)||x))$

• proveable security based on SHA-1 (which is broken atp lol)
• opad and ipad are fixed constants (ipad lol)
• hash of hash → nested hash

Authenticated Encryption

• MAC & Encrypt

• MAC then Encrypt

• Encrypt then MAC → used in practice

• 1 key for encryption/decryption and 1 key for MAC