Set Sizes

index.md

sets topology

---

• [Finite and Infinite sets](#finite\ and\ infinite\ sets)
• [Countable Sets](#countable\ sets)
  • Motivation
  • Counting
    • What is size of a set
    • Cantor-Schroden-Bernstein Theorem
  • Countability
    • What is a countable set
  • Some Properties
• [Uncountable Sets](#uncountable\ sets)
  • Cantor’s Diagonal argument
  • Power set theorem
• Problems

Best Resource: Topology, University of Toronto

---

Finite and Infinite Sets

Size of a set: The size of a set can be defined in many ways. The most common would be the number of elements in the set

$$\begin{array}{r}A=\{a_1,a_2,a_3,a_4,\dots ,a_n\}\\ |A|=n\end{array}$$

Finite Set $\to$ $n<\infty$ Infinite Set $\to$ $n=\infty$

Countable Sets

Motivation

In many areas of math we deal with a lot of infinite, and it becomes important to know when some are larger than others

Countably infinite sets are “small”, and in fact are the “smallest infinite sets”. They become convenient because you can list their elements, and thus use them for inductive proofs.

Counting

With finite sets we take counting for granted: we say that there are 3 birds, or 7 elements etc. But in math counting is defined as a process of comparing sets.

Say you have a hats, and b people. You start placing your hats on the people, and thus you can compare if you have more hats, or more people.

Set Size: Given two sets $A$ and $B$ we say that $|A|\le |B|$ if there exists an injection (one-to-one) $f:A\to B$ or equivalently if there exists a surjection (onto) $g:B\to A$ if there is an injection from $A$ to $B$ but NO surjection from $B$ to $A$ then we can say $|A|<|B|$

Now what would could we say if there were both injections as well as surjections from $A\to B$ ?

$Canter-Schr\ddot{o}der-Bernstein$ Theorem: Given sets $A$ and $B$; $|A|=|B|$ if and only if there exists a bijection (one-to-one and onto) $h:A\to B$

Proving this uses a very useful Proof Techniques called the “back-and-forth argument”

Countability

Countable Sets: A set $A$ is said to be countably infinite if $|A|=|\mathbb{N}|$ and countable if $|A|\le \mathbb{N}$ Note: $\varphi$ is countable because the empty function $f:\varphi \to \mathbb{N}$ is an injection

The intuition behind this should be that if you can list ALL the elements of $A$ in a list as shown then $A$ is countably infinite

$$a_1,a_2,a_3,\dots$$

then you can construct the bijection $f(n)=a_n$ making $|A|=|\mathbb{N}|$

Some Results on Countable Sets

Property 1: Let $A$ be a countably infinite set and $B$ be an infinite subset of $A$. Then $B$ is countable.

Proof: Let $f:\mathbb{N}\to A$ be the bijection proving $A$ is countable. Prove that: there exists a bijection $g:\mathbb{N}\to B$

Let $k_1=\min \{k\in \mathbb{N}:f(k)\in B\}=\min (f^{-1}(B))$ That is, $k_1$ is the smallest number that got mapped into B by the bijection $f:\mathbb{N}\to A$ as $B\subseteq A$

Proof by induction:

base case: define $g(n)$ such that $g(1)=f(k_1)$

inductive step (strong induction): assume we have defined $g(1),g(2),g(3),\dots ,g(n)$. Then let

$$k_{n+1}=\min \{k\in \mathbb{N}:f(k)\in B-\{g(1),g(2),\dots ,g(n)\}\}$$

we can then define $g(n+1)=f(k_{n+1})$ and continue like this by induction to map all elements in B.

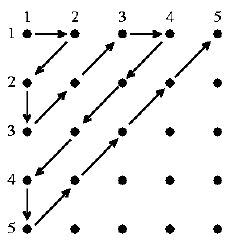
Property 2: Let $A$ and $B$ be countable sets, then $A\times B$ is also countable

We can see this from an image proving $\mathbb{N}\times \mathbb{N}$ is countable

or more rigorously let $f:\mathbb{N}\times \mathbb{N}\to \mathbb{N}$ be

$$f(n,m)=2^n{3}^m$$

which is injective by the uniqueness of prime decompositions

Property 3: A countable union of countable sets is countable. i.e. if $A_i,i\in \mathbb{N}$ are countable sets then ${\bigcup }_{i\in \mathbb{N}}{A}_i$ is countable

let $f_n:\mathbb{N}\to A_n$ be a bijection witnessing that $A_n$ is countable, and define $g:\mathbb{N}\to {\bigcup }_{n\in \mathbb{N}}{A}_n$ by $g(n,i)=f_n(i)$

Uncountable Sets

another good resource: JL Martin

Cantor’s Diagonalization Proof: $(0,1)\subseteq \mathbb{R}$ is uncountable

This is a proof by contradiction

let us assume that $(0,1)$ is countably infinite. And every $x\in (0,1)$ can be represented as $0.a_1{a}_2{a}_3{a}_4{a}_5{a}_6\dots$

let us list the real numbers as $x=f(n)=0.x_1^n{x}_2^n{x}_3^n{x}_4^n{x}_5^n{x}_6^n\dots$

this gives us a table like

we can now construct a number $y=0.y_1{y}_2{y}_3{y}_4{y}_5\dots$ that can not be on our list, which will contradict the assumption that $f(n)$ is a bijection

let $y_k=(x_k^k+1)\mathrm{mod}10$

now $y$ can not be the first number as $y_1\ne x_1^1$ or the second number and so on, essentially $y$ can not be in the table we constructed, thus $f(n)$ can not be a bijection and $(0,1)$ is uncountable

From this we can prove that $\mathbb{R}$ is uncountable

$\mathbb{R}$ is uncountable: we need a bijection $h:(0,1)\to \mathbb{R}$. $f(x)=\pi (x-\frac{1}{2})$ is a bijection from $(0,1)\to (-\frac{\pi }{2},\frac{\pi }{2})$ and $g(x)=\tan x$ is a bijection from $(-\frac{\pi }{2},\frac{\pi }{2})\to \mathbb{R}$. Thus $h(x)=gof(x)$ is our required bijection.

$$h(x)=\tan \pi \left(x-\frac{1}{2}\right)$$

is the required bijection

Power Set Theorem: $|S|<|\mathcal{P}(S)|$

Prove that $f:A\to \mathcal{P}(A)$ can NOT be surjective define a set $D=\{x\in A:x\notin f(x)\}$

assume $f$ is surjective now $D\in \mathcal{P}(A)\therefore \text{range of }f\text{ contains }D$ so let $a\in A:f(a)=D$.

• if $a\in D$ ⇒ $a\in f(a)$ ⇒ $a\notin D$ contradicting the assumption that f is surjective
• if $a\notin D$ ⇒ $a\notin f(a)$ ⇒ $a\in D$ also contradicting itself $\therefore f$ can not be a surjection

$|\mathbb{N}|<|\mathcal{P}(\mathbb{N})|<|\mathcal{P}(\mathcal{P}\mathbb{N}))|\dots$ there are infinitely many sizes of infinity