Greedy

Algorithms

• Greedy
  • [Exchange Arguments](#exchange\ arguments)
  • [Greedy stays ahead](#greedy\ stays\ ahead)
  • [fractional knapsack](#fractional\ knapsack\ problem)
  • activity selection
  • interval scheduling
  • [huffman encoding](#huffman\ encoding)

---

Proving that the greedy algorithm is optimal:

• Exchange Arguments
• Greedy stays ahead

Exchange Arguments

Consider any possible solution to the problem and gradually transform into the solution found by the greedy algorithm without hurting its quality eg Problem: schedule $n$ jobs with deadlines $d_i$ and length $t_i$ to a machine that can only do one job at a time Greedy Solution: Earliest Deadline First. Sort jobs in increasing order of deadlines and schedule jobs in that order Exchange Argument Proof: Consider an Optimal Solution $O$. The optimal solution will not allow the machine to ever be idle Let us an define an inversion as $jo{b}_i$ being scheduled before $jo{b}_j$ despite $d_j<d_i$

• the greedy solution will have no inversions

to prove: there is an optimal solution with no inversions and no idle time

it is trivial to say the optimal solution has no idle time

swapping an adjacent inverted pair does not affect the finishing time of any other tasks, and also reduces task $j$‘s lateness. We only need to check the lateness of task $i$ then.

The point to note is that lateness of $i$ can not be more than the lateness of $j$ before swapping

$l_i(\text{after swap})=f(j)-d_i<l_j(\text{before swap})=f(j)-d_j$

therefore the overall lateness is being reduced

Here swapping is the transformation we are doing to our “optimal” solution to make it align with the greedy solution while not losing its optimalness

---

Greedy Stays Ahead

consider the optimal solution with compatible tasks with finish times and all tasks being compatible

obviously $f(i)\le f(j)$

now our greedy solution always prioritizes choosing the minimum $f(j)$ after job $i$ is done. This means that at worst it always has the option of choosing job $j$ if not a job $k$ with $f(k)\le f(j)$ therefore our greedy solution stays ahead of the “optimal” one.

---

Fractional Knapsack Problem

Problem Given objects with a certain value and weight, and a container with capacity, how do you choose which objects to take to maximum the value in the container. You can break objects for partial value.

Solution You sort the objects by ratio of $value/weight$ and add the highest ratioed object or whatever fraction of it you can

---

Huffman Encoding

consider a string with $n$ unique characters each with a frequency $f_i$ sort the characters in increasing order of $f_i$ build a bottom up tree

• choose the 2 elements with the least frequency (first two elements)
• put them in 2 leafs and have their root be their combined frequency
• put this combined frequency back in the sorted list of $f_i$ and repeat

Huffman (C)
n = C.length // no. of unique characters
Q = C
for i = 0 to n - 2
	allocate new node z
	z.left = x = Extract-Min(Q)
	z.right = y = Extract-Min(Q)
	z.freg = x.freq + y.freq
	insert(Q, z)
return Extract-Min(Q) // this is the root

below is an image for the input

C	C.freq
o	1
u	1
x	1
p	1
r	1
l	1
f	3
s	2
h	2
i	2
m	2
t	2
n	2
’ ‘	7
a	4
e	4

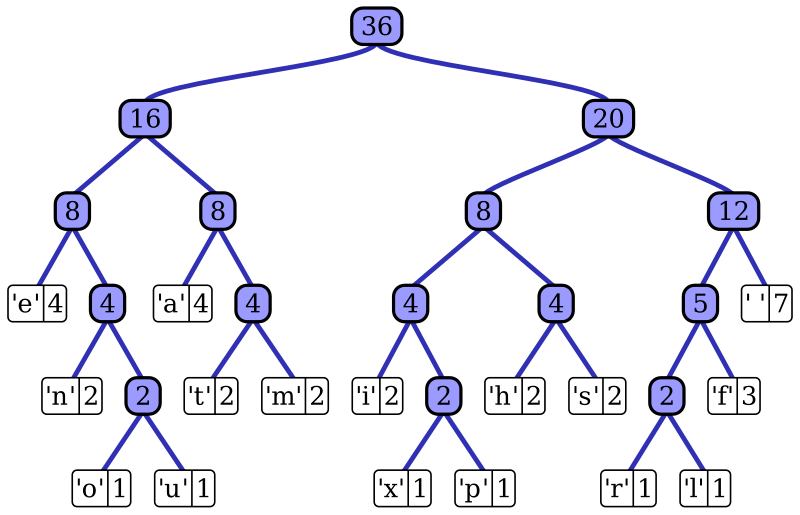
to create the huffman code starting from the root traverse to each leaf. Assign a $0$ to each left node and a $1$ to each right node. The huffman code for each character will be string encountered as you traverse from root to leaf

---